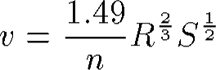GLG 410 Programming Matlab
In this week's lab, I would like for you all to build a couple of functions
that make some interesting geomorphic calculations.
Following the lecture examples
as well as the information from the
handouts from Mastering Matlab 5, do the following tasks and prepare a
web-based presentation of the answers. Email the url to Jason and I by
the beginning of lab on Tuesday November 30:
River discharge function
The volume of water that passes by a point in a river over a certain time
increment is the discharge (for example, the Tempe Town Lake can apparently
withstand about 40,000 cubic feet per second with the dams up). THe
dischage can be simply expressed as the product of the velocity times the
cross-sectional area of the flow:
Q = v * A, where Q is discharge [L^3/T], v is velocity [L/T], and A is
area [L^2]
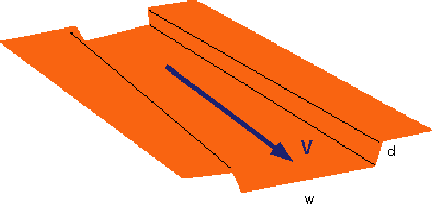
Many channels are effectively rectangular, so we can express the
cross-sectional area as the product of width (w) times depth (d):
A = w * d
So how to calculate the velocity?
We use a simple formulation called Manning's eequation that relates the
flow velocity to the local channel slope (s [dimensionless]), a channel
shape parameter called the hydraulic radius [L]--see below, and a roughness
parameter n [L^1/6]. NOTE THAT THIS IS FOR ENGLISH UNITS (feet,
seconds):
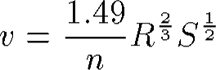
The hydraulic radius R is equal to the ratio of the channel area (A) to
its wetted perimeter (P):
P = w + 2d
R = A/P
The Manning roughness coefficient (n) is estimated based upon
inspection of the channel and its shape. Here is a table of roughnesses
depending on the channel boundary type.
Tasks
1) Develop a well documented Matlab function that will calculate the
velocity and the discharge at a point given the channel shape, roughness,
and slope parameters. This should be presented on your web pages with a
link to an html version of the entire function.
2) Make a plot of the relationship of velocity versus channel slope for
values of slope varying from 0 to 0.2 (about 12 degrees), all other
variables constant. How does
velocity vary with channel slope?
3) Make a plot of the relationship between velocity and hydraulic
radius, all other
variables constant. Choose a range of radius values that are for shallow and deep
channels. All things being equal, is the velocity faster in a deeper or
shallower channel?
4) Make a plot of the relationship between velocity and channel roughness, all other
variables constant. Vary the roughness from that of a smooth glass chute
to a mountain stream. How does the velocity vary with roughness?
5) If you were to be watching the Salt River at the downstream end of the
Tempe Town Lake and the water were flowing across the location of the downstream
dam that is 19' high and the channel width is about 850' and the channel
slope there is 0.0013 (Arrowsmith actually calculated based on surveyed
elevations in the channel), what would the flow velocity and discharge
be (you estimate the roughness)?
6) If you were watching the Salt River at the downstream end of Tempe
Town Lake and the water were bank full (to the top of the levees=40'), the
channel width were 900' and the slope was the same as above, what would
the discharge and velocity be (you estimate the roughness)? In 1993, the
river was supposedly flowing at 100,000 cubic feet per second. Based upon
your calculations, was it at bankfull?
Pages maintained by
Prof. Ramón Arrowsmith
Last modified November 28, 1999